샘플 사이즈·누락 자료 등 찾아봐야 정확해
[에듀 포스팅] 대입 통계자료 제대로 이해하기
통계 오류에는 통계 자체의 오류, 자료 수집의 오류, 자료 누락의 오류, 해석의 오류 등 여러 단계가 있다. 벤저민 디즈레일리는 1891년 “세상에는 3가지 거짓말이 있다. 그럴 듯한 거짓말, 새빨간 거짓말, 그리고 통계”라고 말했다. 미국의 천체물리학자 클리퍼드 스톨은 “데이터는 정보가 아니고 정보는 지식이 아니며 지식은 이해가 아니고 이해는 지혜가 아니다"라고 말했다. 학부모가 새겨 볼 만하다.
▶데이터 해석 오류들
-같은 공식, 다른 집단:UCLA의 2019년도 신입 지원생들의 합격률은 12%다. 총 11만1322명이 지원하고 1만3720명이 합격했으니 (최종 등록생은 5920명) 정확한 데이터다. 같은 해 하버드 2020년도 조기지원 합격률은 13.9% 로 나타났다. 6424명이 지원했고 895명이 합격했다. 합격자수를 지원자수로 나눠 백분율을 구하는 공식은 양쪽이 같다. 대략 8.3대1 과 7.2대1 이니까 엇비슷하기도 하다. 심지어 UCLA 합격률이 하버드 합격률보다 낮으니 UCLA에 들어가기가 하버드 조기전형으로 들어가기보다 어렵다고 말할 수 있다. 그런데 알다시피 그게 꼭 그렇지는 않다. 지원자풀이 다르기 때문이다. 이는 마치 수술후 생존률이 100%에 육박하는 성형외과의사와 훨씬 낮은 응급외상센터 외과의사 중 어느 쪽이 실력이 좋은지 비교하는 것과 같다.
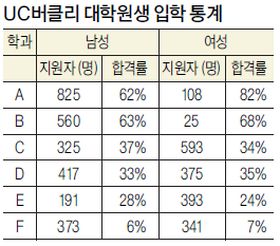
-총합의 통계와 세부적 통계의 괴리:통계 수치는 완벽하더라도 해석에 오류가 따르거나 오해할 수 있다. 예를 들면 ‘심슨의 역설'이다. 총체적인 통계가 실상은 세부 집단에서는 전혀 그렇지 않을 수 있다는 의미다. 가장 쉬운 모델은 이런 것이다. P.J. 비켈, E.A. 하멜, J.W. 오코넬(1975년)이 제시한 '대학원 입학심사 과정에서의 성적 차별: 버클리'통계다.
UC버클리가 1973년 대학원생 선발에서 여성을 심각하게 차별한다는 데이터로 지원한 남학생의 44%가 합격한 반면에 여학생은 35%로 나왔다. 그런데 통계를 들여다 보면 해석이 다르다. <표 참조>
-상관관계와 인과관계:통계를 보면서 현상을 분석할 때 상관관계가 있다고 해도 인과관계가 아닐 수 있다. 예를 들면 한 학교에서 AP 과목 수와 대입 합격률로 통계를 만들었더니 AP 과목 수가 높을수록 지원한 학교에 합격할 확률이 적더라는 완벽하고 믿을 만한 상관관계가 있었다. 그렇다면 합격률을 높이기 위해 AP를 덜 택하는 게 좋을까? AP 과목을 많이 택한 학생들은 우수 학생들로서 주로 합격률이 낮은, 즉 경쟁률이 높은 명문대에 지원하였고 당연히 합격하는 대학도 있지만 불합격하는 학교들도 많았다. AP 과목을 택하지 않은 학생들은 주로 경쟁률이 낮고 합격률이 높은 로컬 주립대학을 지원해 대부분 합격했다. 이런 경우 분명히 상관관계는 있었으나 인과관계를 나타내는 것이 아니다. 이렇게 예시가 분명한 오류를 발견하기 쉬운 경우만 있는 것은 아니다. 상당히 그럴듯하게 인과관계가 있는 것처럼 다수의 관찰자에게 보이는 경우가 많기 때문에 데이터를 분석관은 선입관을 갖고 부주의할 경우 어처구니 없는 오류성 내용이 대중에게 사실로 전파될 가능성은 언제나 존재한다. 검증과 주의가 필요한 이유다.
-과적합의 오류:명문대 지원생들이 주로 SAT 고득점자들이고 명문대 합격자들의 평균 SAT 점수가 높다보니, SAT 점수가 좋아야 합격할 것이라는 생각이 해당된다. SAT 고득점은 일종의 기본사항이며 합격 불합격에 중요한 요소가 아님에도 점수가 좋으면 마치 합격할 수 있다는 생각을 한다. 그러나 알다시피 미국 대학들은 학생을 뽑는 데 사용하는 요소들은 이렇게 간단하지 않다, 단순히 나열만 해도 학과목수준, AP 개수, GPA, 특별활동의 수와 질, 학교 수준, 대입시험(SAT) 점수와 각 과목의 점수, 가족구성, 경제상황, 지역, 추천서, 에세이 등이다. 이 모든 것은 수치로 나타낼 수 없다. 그러나 각 요소들을 포뮬라로 만들려는 시도가 과적합(Over-fitting)의 오류를 만들어낸다.
-작은 샘플:통계는 주로 샘플이 클 수록 정확하다. 학년별로 학생수가 적은 학교일수록 작년에 있었던 일이 올해 일어날지 조심해서 예측해야 한다. 예를 들면, 한 학년이 1000명인 고등학교에서 지난 5년간 매년 1등에서 20등까지 20명씩 UCLA에 진학하고 있다면, 내가 몇 등이냐가, 내가 올해 그 대학에 합격할 지를 상당히 높은 확률로 보여줄 수 있다. 그러나 한 학년이 50명인 학교에서 5년 만에 1명이 합격했지만 등수를 알 수 없다거나 합격한 이유를 잘 모른다면 올해도 이 학교에서 합격생이 나올 것인지 1등을 한다면 가능성이 높아질 것인지는 예측하기 힘들다. 두 경우다 해당 학교의 합격률은 2%이지만 통계로 예측이 정확히 가능한 경우와 거의 불가능 경우의 극단적 예시이다.
-25th~75th 퍼센타일:신입생 SAT 점수 분포로 사용되는 이 수치는 오직 짐작용일 뿐이다. 예를 들어서 1390~1580점이라면 정확한 해석은 신입생의 상위 25%는 1580점 이상이며 하위 25%는 1390점 미만이라는 것이다. 그리고 1390~1580점 사이에 나머지 50%의 학생이 있다는 사실이다. 1580점이라는 숫자는 만점에 매우 가깝기 때문에 4분의 1이나 되는 학생들이 거의 만점이나 다름 없다는 것을 알 수 있다. 이렇게 한쪽에 점수가 치우쳐 있다면 중간 점수 학생들의 다수도 1390점 쪽보다는 1580점 쪽으로 치우쳐 있으리라고 짐작하는 것이 현명하다. 즉 1485점이 평균이라거나 중간 점수일 것이라는 짐작은 덜 이성적이고, 내 점수가 1480점이니까 중간은 했다고 보기는 무리가 있다. 극단적인 경우 중간 50%의 대부분은 1550점 이상이고 하위 25% 학생이 1390점일 수도 있다. 이와달리 점수분포도가 1250~1430점의 학교라면 합격생의 평균 점수도 낮다고 추측할 수 있다.
양 민 원장 / 닥터양 에듀콘 dryang@dryang.us










with the Korea JoongAng Daily
To write comments, please log in to one of the accounts.
Standards Board Policy (0/250자)